Research

Representation learning in reinforcement learning

Stochastic nonlinear control, even with known dynamics and rewards, remains a difficult problem with limited efficient algorithms. While deep reinforcement learning (RL) has advanced the field, these methods often lack rigorous theoretical guarantees and require complex tuning. In this line of work, we take a representation-based viewpoint to reinforcement learning, by using finite-dimensional spectral features for representing value functions via computing spectral decompositions of the transition operator. This approach, based on recent work in linear MDPs, enables more efficient single-agent RL algorithms with strong theoretical guarantees. Beyond the single-agent setting, our approach also scales to continuous state-action network multiagent control, demonstrating success in applications such as Kuramoto frequency synchronization and building heating control. I believe that representation learning has great potential to significantly improve sample efficiency in reinforcement learning, and there are many open questions both theoretically and in practice which I am currently actively exploring. For instance, can we design simple yet effective representation learning algorithms in the model-free case? How can we apply such methods to enable more tractable control in high-dimensional problems such as fluid control?

Selected work:

Designing sample-efficient optimization and control tools for bioengineering

Integrating AI, machine learning and feedback control into bioelectronics systems is one of the most exciting challenges facing us today. Can we enable real-time control of biological systems and improve their functionality, despite limited prior knowledge of the underlying dynamics? In a recent collaborative work with my wonderful bioelectronics colleagues at Prof Jia Liu’s lab, I worked on designing AI-based methods to achieve adaptive electrical impulse control to accelerate the maturation of cardiac organoids. Sample efficiency is of paramount importance in this project, since we have limited available experimental resources, and an experiment takes a long time to complete (around two months). Utilizing the fact that we can run several experiments together in parallel, we adapted a batch Bayesian optimization framework to model and approach the organoid maturation problem in a sample-efficient fashion. Compared with an existing heuristic policy, the policy learned by our algorithm not only significantly speeds up the maturation process of the organoid tissue, but leads to a better final maturation level at the end of the experiment.

Besides cardiac organoid maturation, there are many problems in bioengineering (and beyond) that I believe can be fruitfully tackled by intelligently integrating machine learning and control techniques with (possibly limited) domain knowledge and insight. I am interested and motivated to continue interdisciplinary collaboration that can jointly advance our understanding of bioengineering, science and AI.

Selected work:

An AI-cyborg system for enhancing organoid maturation

Ren Liu*, Zhaolin Ren*, Xinhe Zhang*, Qiang Li, Wenbo Wang, Zuwan Lin, Richard T. Lee, Jie Ding, Na Li, Jia Liu

Preprint available soon.

Theory and practice of model-free optimization

In many real-life problems, we may only be able to learn about a system through limited interactive feedback, with no knowledge of the exact form of the underlying dynamics. In optimization and control problems involving such systems, we do not have direct access to the gradients underpinning these problems, making it difficult for us to apply plug-and-play gradient-descent/ascent type methods which are the workhorse of modern machine learning. Instead, to optimize and control these systems, we need to leverage gradient-free optimization techniques, such as zeroth-order optimization and Bayesian optimization. For zeroth-order optimization, I have worked on theoretical guarantees for the ability of two-point zeroth-order algorithms to escape saddle points. This work was inspired by my interest in better understanding the convergence properties of two-point zeroth order gradient estimation, which is an important method often used in practice. For Bayesian optimization (BO), sample efficiency is often paramount as data collection can be expensive both in terms of time and cost; the cardiac tissue maturation project I discussed earlier is a great example. Can we leverage parallel/batch learning techniques to enable more efficient learning? In contrast to standard BO, batch BO presents both advantages (sampling more points per round) and questions (how to intelligently choose the points to sample every round whilst avoiding redundancy?). However, there is a dearth of efficient yet provable batch Bayesian optimization algorithms. To overcome this, I designed a novel batch BO algorithm, called TS-RSR, which samples a batch at each round by minimizing a term which refer to as TS-RSR (Thompson Sampling - Regret to Sigma Ratio). It avoids several of the practical problems faced by existing theoretical-backed algorithms such as Batch Upper-Confidence Bound (BUCB) and Thompson Sampling (TS), such as sensitivity to hyperparameter tuning and lack of redundancy avoidance, but also satisfies a rigorous convergence bound. In practice, we found that our algorithm achieves state-of-the-art performance on a range of synthetic and realistic test functions.

Selected work:

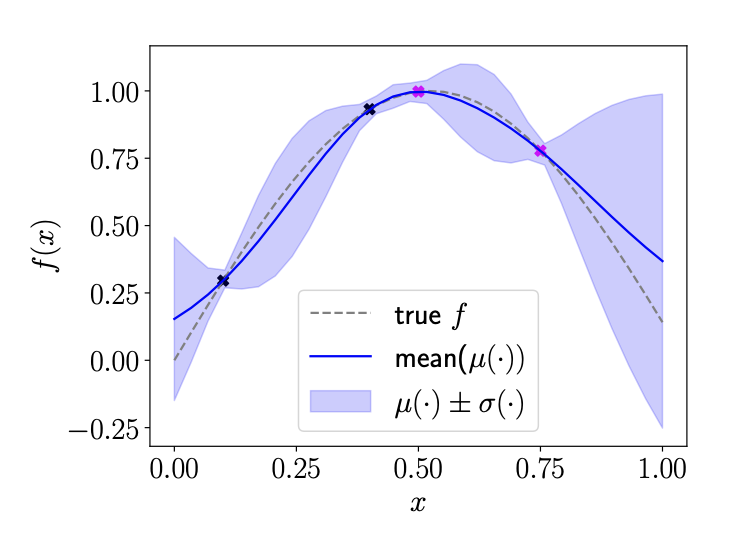
TS-RSR: A provably efficient approach for batch bayesian optimization

Zhaolin Ren, Na Li

Under review at the SIAM Journal for Optimization.

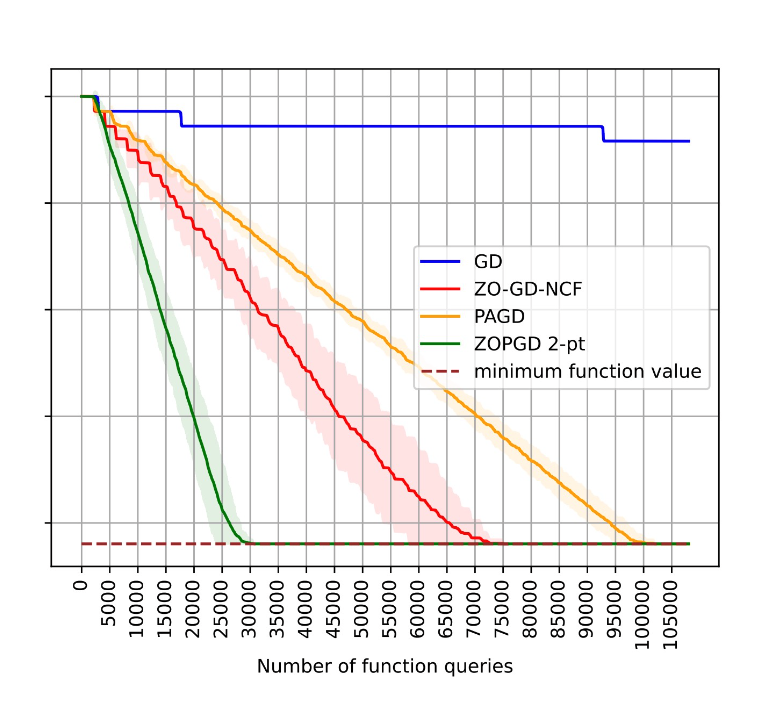
Escaping saddle points in zeroth-order optimization: the power of two-point estimators

Zhaolin Ren, Yujie Tang, Na Li

International Conference on Machine Learning 2023.